This attractor¹ was found by William Finlay Langford in 1984.² As the title of his paper suggests, the attractor is a bifurcation of a torus. What does that mean? Well, what he has done is taking a system of differential equations that resulted in a torus shape and simply added a bifurcation term to one of them. Jokes aside, he has probably done a lot more work to get to that point but looking at the equations and tinkering with the parameters let you imagine just that. Specifically, this term is \(\varepsilon\, z\, x^3\) and it is added to \(\dot{z}\). If you leave it out by setting \(\varepsilon = 0\), you get a spiraly donut shape³:

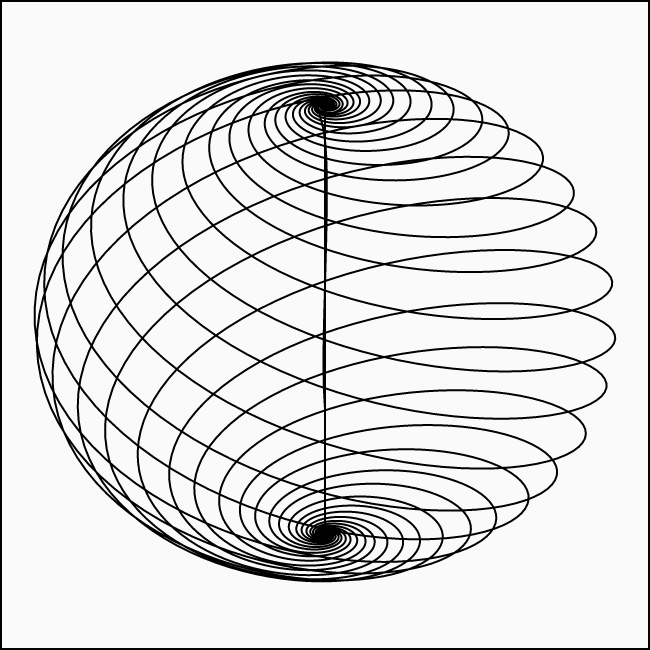
The inner tube is very thin here but when decreasing \(\alpha\) to something like \(0.65\), the shape becomes obvious:

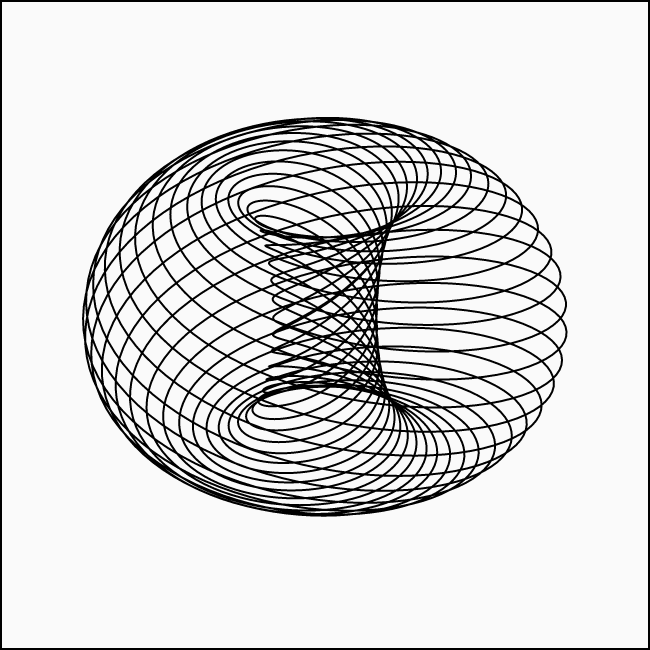
Now when increasing the bifurcation parameter (and keeping the original value for \(\alpha\)), the chaos begins. Here is it with \(\varepsilon = 0.001\) and as you can see, this very slight change pushes the system out of symmetry:

Renders

Differential system:

\[\dot{x} = x\, (z - \beta) - \omega\, y\] \[\dot{y} = y\, (z - \beta) + \omega\, x\] \[\dot{z} = \lambda + \alpha\, z - \frac{z^3}{3} - (1 + \varrho\, z)\, (x^2 + y^2) + \varepsilon\, z\, x^3\]

Constants:

\[\alpha = 0.95\] \[\beta = 0.7\] \[\lambda = 0.6\] \[\omega = 3.5\] \[\varrho = 0.25\] \[\varepsilon = 0.1\]

---

1. Most online resources refer to this attractor as the “Aizawa Attractor” despite that Yoji Aizawa (it apparently got named after) seems to have nothing to do with it.⁴ How this confusion arose is unclear. ↩

2. W.F. Langford, 1984. "Numerical Studies of Torus Bifurcations". In: T. Küpper, H.D. Mittelmann, H. Weber (eds), "Numerical Methods for Bifurcation Problems". International Series of Numerical Mathematics, Vol 70. doi:10.1007/978-3-0348-6256-1_19. ↩

3. This and the other simple images were generated using Processing, similar to this one I’ve done for the Lorenz Attractor. ↩

4. This was pointed out by: E. Fleurantin, J.D. Mireles James, 2019. "Resonant tori, transport barriers, and chaos in a vector field with a Neimark-Sacker bifurcation". Department of Mathematics, Florida Atlantic University. ↩