Originally proposed by the biologist René Thomas (1928–2017), this set of differential equations is cyclically symmetric.¹ The constant \(b\) is a bifurcation parameter that describes how dissipative the system is. Dissipation is a property from thermodynamics that can be thought of as a kind of dampening which is the result of a loss of energy, i.e. in form of heat. Depending on the value of \(b\), the attractor changes its shape. Here is a list of what happens:

• \(b \ge 1\): origin is a stable point
• \(1 > b \gtrsim 0.329\): two stable points
• \(0.329 > b \gtrsim 0.208\): two stable oscillations
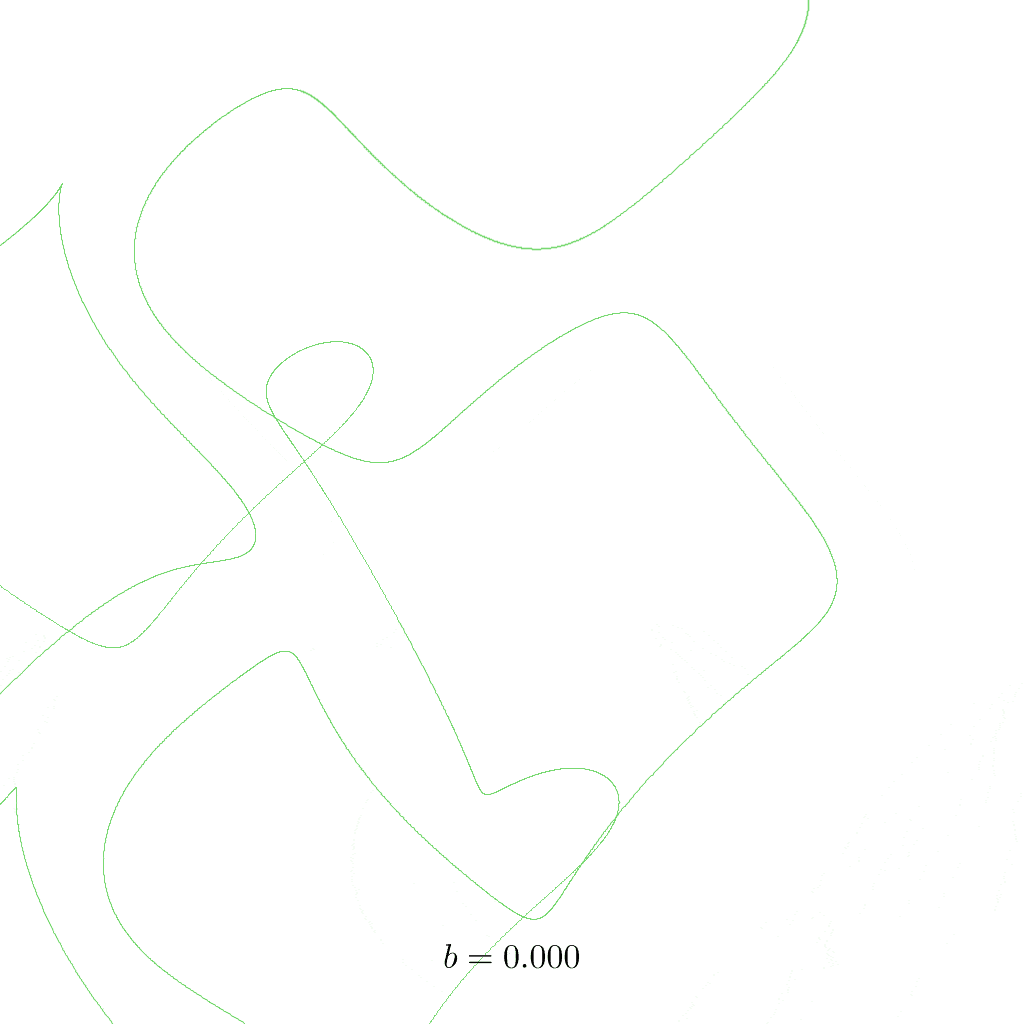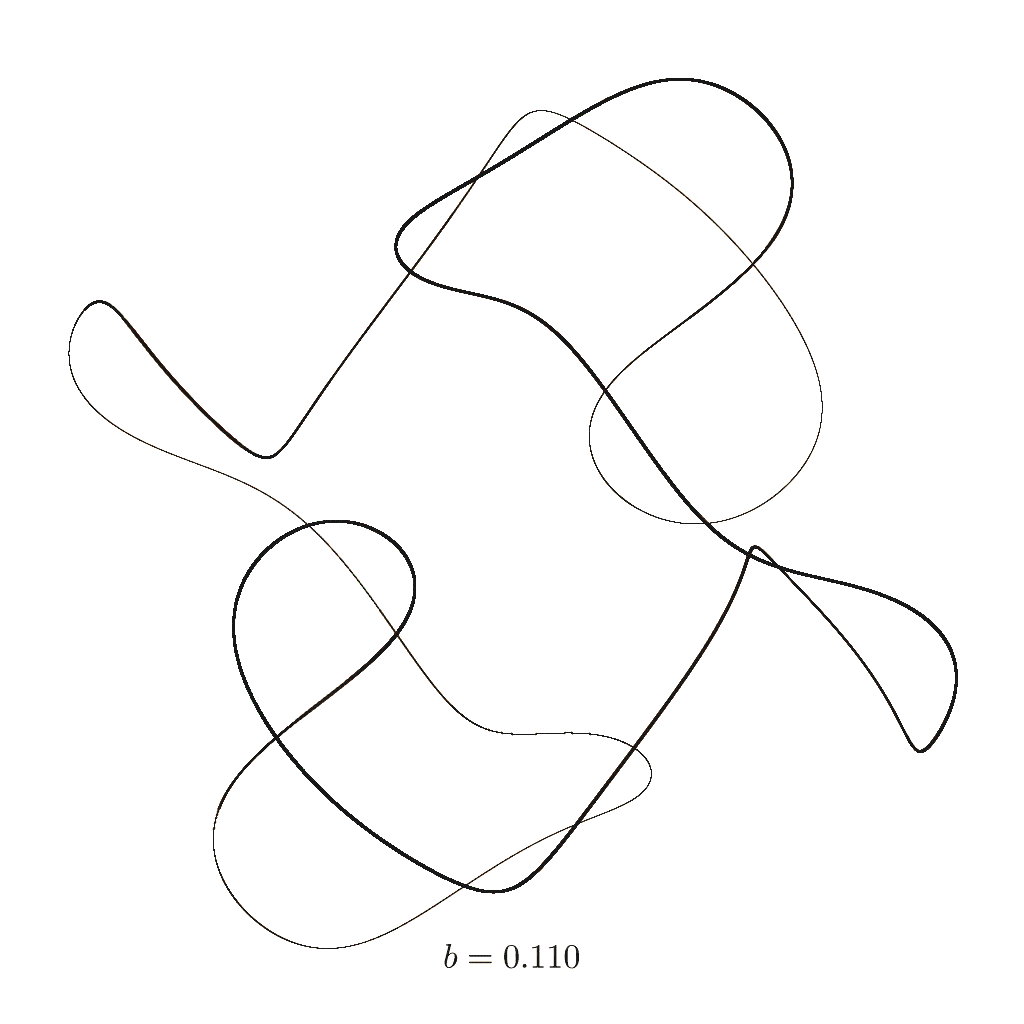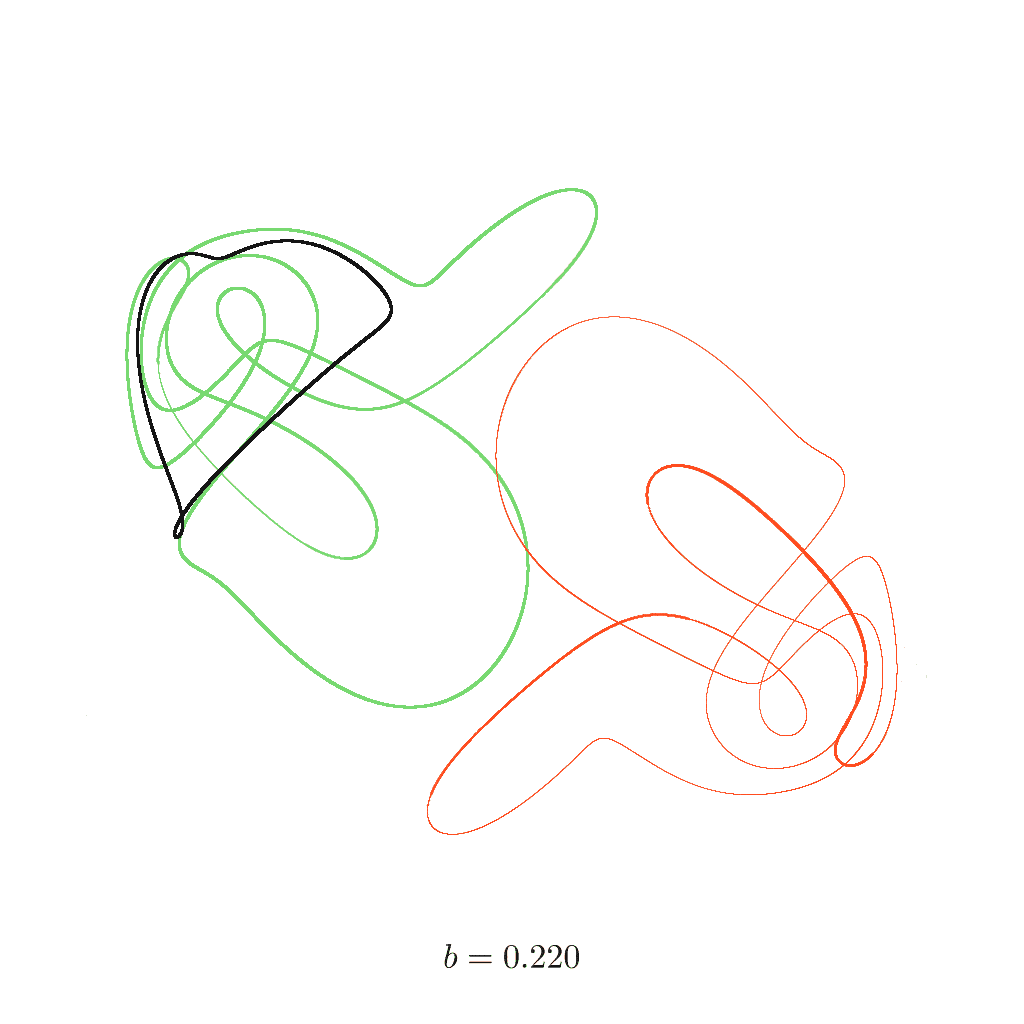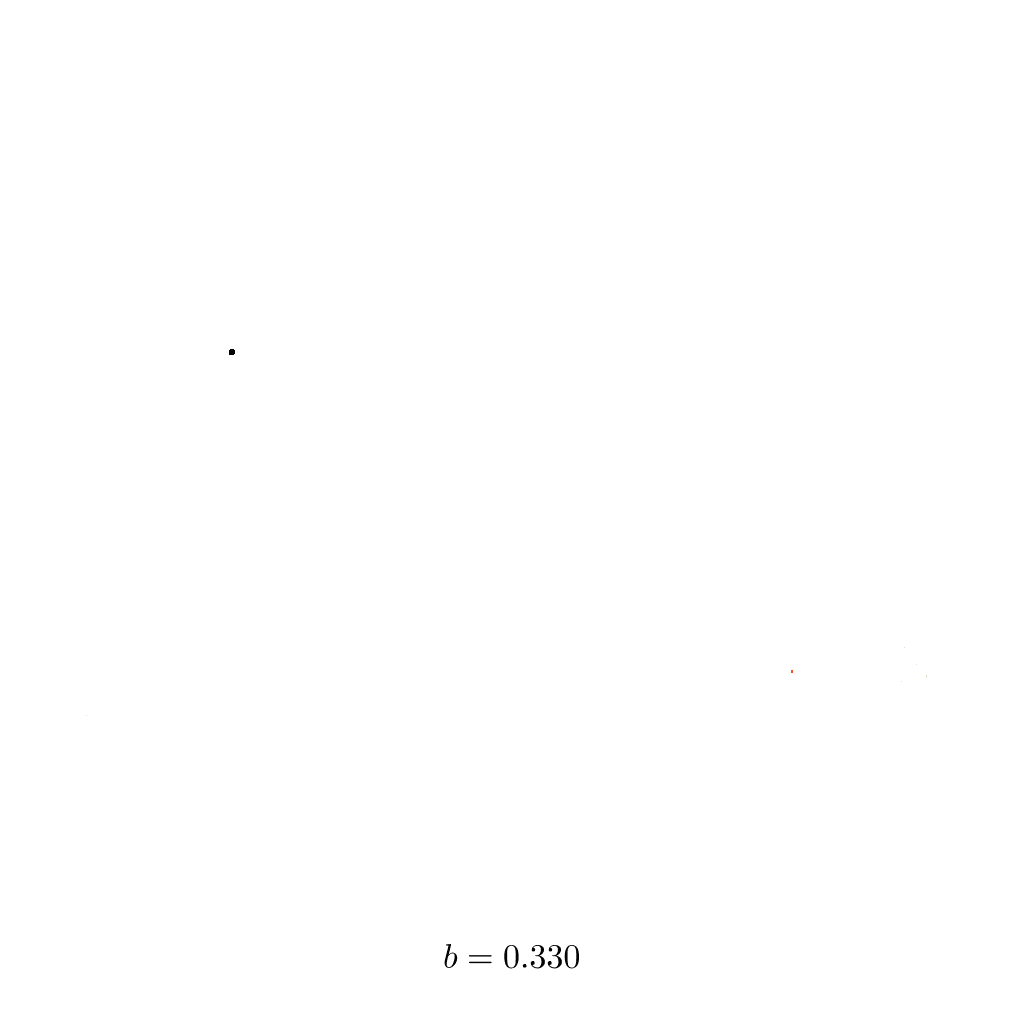
• \(0.208 > b > 0\): mostly chaos
• \(b = 0\): no dissipation, brownian walk into infinity

There are several particularly interesting values for which more than just one attractor stabilise seperately:

• \(b = 0.22\): two cycles
• \(b = 0.19\): single cycle
• \(b = 0.17\): three cycles
• \(b = 0.13\): three cycles

Renders

Differential system:

\[\dot{x} = \sin(y) - b\, x\] \[\dot{y} = \sin(z) - b\, y\] \[\dot{z} = \sin(x) - b\, z\]

Constants:

\[b = 0.19\]

Parameter Animation

In the following animation, the constant \(b\) is slowly increased from \(0\) to \(0.33\) (the points that remain above would be too small to see). Three trajectories are shown that emerge from different starting points:

• green: \((0.1,\; 0,\; 0)\)
• orange: \((0.1,\; 0,\; -0.5)\)
• black: \((0.1,\; 0.5,\; 0)\)

For each of them, \(100000\) time steps are calculated. In order to only show the long-term behaviour of the system, the first \(50000\) points are omitted. The space is rotated a bit to allow a better view of the attractor.

Pay attention to the three trajectories as \(b\) increases – there are moments when you don’t see all three colours because one covers another when they follow the exact same trajectory; sometimes the lines form well defined closed loops; and then you’ll find cases where the overall attractor is clearly visible but the trajectories still variate slightly. You may compare the transitions with the lists above.

At the beginning (for small \(b\)) you see a very random mess of lines, this is when the system is not bounded and all points can freely escape in all directions. Though, the general motion of \(\sin\)-waves is recognisable.

Stereographic Animation

---

1. R. Thomas, 1999. "Deterministic chaos seen in terms of feedback circuits: Analysis, synthesis, ‘labyrinth chaos’". Int. J. Bifurc. Chaos. 09(10). doi:10.1142/s0218127499001383. ↩